Instabilités hydrodynamiques

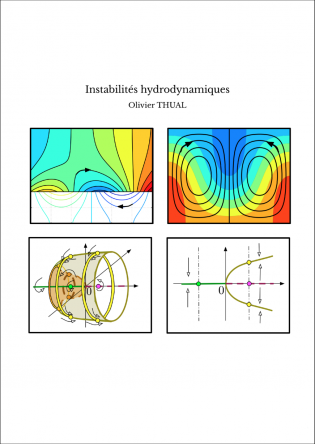
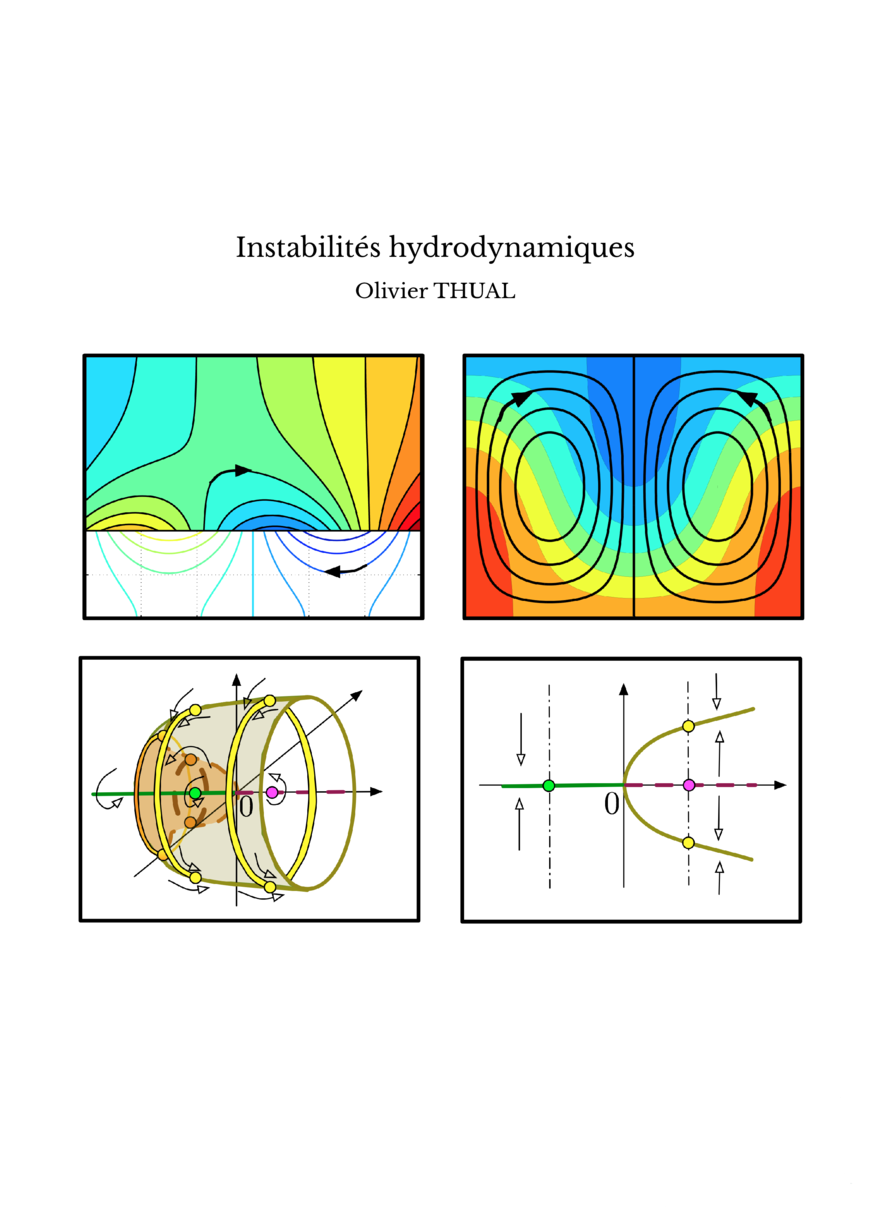
La modélisation consiste à représenter la réalité physique par un système d'équations mathématiques. Cet ouvrage présente les outils qui permettent de déterminer si un équilibre est stable ou instable. Le premier chapitre étudie la stabilité d'un écoulement constitué de deux couches fluides. L'instabilité de Kelvin-Helmoltz apparait lorsque la vitesse d’un fluide léger, surmontant un fluide lourd, est suffisamment forte. Le deuxième chapitre aborde l'exemple de la convection de Rayleigh-Bénard observée lorsque l'on soumet une couche fluide à une différence de température. Dans le dernier chapitre, les notions de base sur la linéarisation des systèmes d'équations autour d'un équilibre sont présentées.